LA TENDENCIA A LA ARMONÍA

Carlos Calvimontes Rojas

.....toda creación artística o científica implica una transición del desorden al orden.

Como hay una tendencia al caos hay una tendencia a la armonía y ambas son esenciales en el diseño del Universo.

Existe la tendencia al caos —medida por la entropía, el grado de desorden irreversible de un sistema—, la propensión de pasar de un estado de orden a uno desorganizado; como existe una tendencia al orden, capaz de modificar el caos mediante un proceso hacia un nuevo orden —donde aparece la neguentropía, la atracción natural hacia la regulación de un sistema— donde impere la armonía.

La tendencia al orden, en lo que es medible, se da en un proceso paulatino hacia un estado de armonía entre las partes de un sistema, satisfactorio para su observación o para los propósitos perseguidos pero no de perfección; en la Naturaleza es imposible encontrar un círculo con el p perfecto u otra forma geométrica que tenga las precisas proporciones del Número de Oro, F.

Es en la geometría donde se puede observar con toda claridad la tendencia al orden, medida con el paradigma de la armonía, el Número de Oro, mediante la observación de la espiral inscrita en un Rectángulo Áureo, que muestra la evolución de la Sucesión o Serie de Fibonacci, en la que se obtiene el Número de Oro —al dividir un número por el anterior— con mayor precisión según avance la Serie.

Pero no es privativo de la Serie de Fibonacci tener esos atributos; se ha encontrado la Serie de Tesla que el célebre inventor pensó y expuso en una frase sobre el 3 - 6 - 9, tergiversada de mil formas hasta llegar a lo esotérico . Aquí se expone las generadas con los dígitos del 1 al 9. La primera Serie (1) es la de Fibonacci, la segunda (2) es la de Tesla y a continuación van las del 3 al 9.

Las series calculadas y otras que se pueden dar con números iniciales de mayor tamaño estarían en ámbitos —que se irán descubriendo— en la Naturaleza o de la obra humana, diferentes al que inspiro a Fibonacci y aunque todas tenderían en su límite infinito al Numero de Oro, justificarían y explicarían la elección de los números iniciales: 3 – 4 - 7, 4 – 5 – 9, 5 – 6 -11, y otros.

Como son series “convergentes” —con términos que se aproximan a un valor específico conforme se progresa—calculadas para obtener un F con un valor de uso corriente, 1,618 con tres decimales, apenas se debe pasar del número situado en el décimo lugar. Pero, para mostrar un mayor acercamiento al valor del número de oro, 1,61803 con cinco decimales, hay que llegar al decimosexto lugar o sobrepasarlo.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…  (1,61803…, de 17/16)

1, 2, 3, 6, 9, 15, 24 , 39, 63, 102, 165, 267, 432, 699, 1131, 1830…  (1,61803…, de 16/15)

1, 3, 4, 7, 11 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2.207…  (1,61803…, de 16/15)

1, 4, 5, 9, 14, 23, 37, 50, 87, 137, 224, 361, 585, 946, 1.531, 2.477, 4.008, 6.485, 10.493, 16.978…  (1,61803… de 20/19)

1, 5, 6, 11, 17, 28, 45, 73, 118, 191, 309, 500, 809, 1309, 2118, 3.427, 5.545, 8.972…  (1,61803…,  de 18/17)

1, 6, 7, 13, 20, 33, 53, 86, 139, 225, 364, 589, 953, 1.542, 2.495, 4.037, 6.532, 10.569…  (1,61803…, de 18/17)

1, 7, 8, 15, 23, 38, 61, 99, 160, 259, 419, 678, 1.097, 1.775, 2.872, 4.647, 7.519, 12.166…  (1,61803…,  de 18/17)

1, 8, 9, 17, 26, 43, 69, 112, 181, 293, 474, 767, 1.241, 2.008, 3.249, 5.257…  (1,61803…, de 16/15)

1, 9, 10, 19, 29, 48, 77, 125, 202, 327, 529, 856, 1.385, 2.241, 3.626, 5.867, 9.493... (1,61803…,  de 17/16)

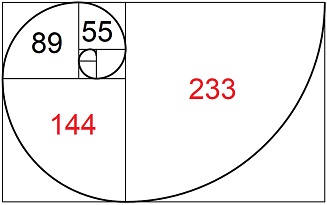
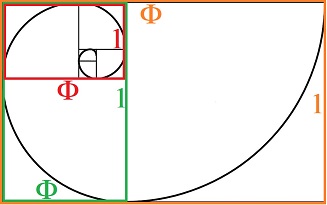
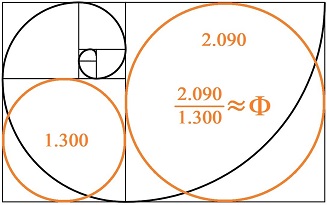
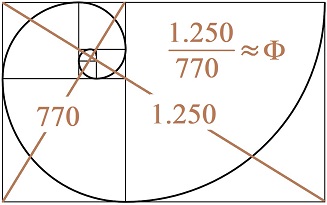
Lo expuesto se demuestra y explica mediante el valor de cada tramo de la Espiral Dorada, tomando como ejemplo los números (233/144) que dan un F de 1,618… en la Serie de Fibonacci; y, por las dimensiones perimetrales de dos formas geométricas y las líneas (con la misma escala) contenidas en partes del Rectángulo Áureo y cuyo cociente da el valor usual de F.